问题
计算题
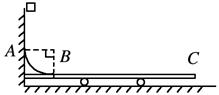
如图所示，水平地面上固定着一辆小车，左侧靠在竖直墙壁上，小车的四分之一圆弧轨道AB是光滑的，在最低点B与水平轨道BC相切，BC的长度是圆弧半径的10倍，且圆弧半径为R，整个轨道处于同一竖直平面内，可视为质点的物块从A点正上方某处无初速下落，恰好落入小车圆弧轨道上滑动，然后沿水平轨道滑行到轨道末端C，速度恰好为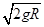
。已知物块到达圆弧轨道最低点B时对轨道的压力是物块重力的9倍，不考虑空气阻力、墙壁的摩擦阻力和物块落入圆弧轨道时的能量损失．求：
（1）物块开始下落的位置距水平轨道BC的竖直高度
（2）物块与水平轨道BC间的动摩擦因数μ
答案
（1）h＝4R（2）μ＝0.3.
题目分析：由题意，对m从开始下落到圆弧轨道最低点的过程中机械能守恒，有
mgh＝
mv2
在圆弧轨道最低点由牛顿第二定律，对m有
9mg－mg＝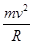
解得h＝4R.
(2)由题意有f＝μmg
对物块，根据动能定理有：－f×10R＝mv′2－mv2
联立上述方程式，代入数据解得μ＝0.3.
点评：本题难度较小，首先应建立模型，分析运动情况，选择合适的运动过程作为研究对象