问题
解答题
若x、y满足(x-1)2+(y+2)2=4,求S=2x+y的最大值和最小值.
答案
S的最大值是2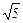 ,最小值为-2
,最小值为-2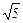 .
.
由(x-1)2+(y+2)2=22可知,它表示以(1,-2)为圆心,半径等于2的圆.
令x=1+2cosθ,y=-2+2sinθ,
则S=2x+y=2+4cosθ-2+2sinθ=4cosθ+2sinθ.
∴|S|≤ =2
=2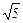 ,
,
即-2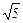 ≤S≤2
≤S≤2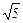 .
.
∴S的最大值是2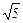 ,最小值为-2
,最小值为-2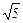 .
.
若x、y满足(x-1)2+(y+2)2=4,求S=2x+y的最大值和最小值.
S的最大值是2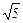 ,最小值为-2
,最小值为-2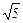 .
.
由(x-1)2+(y+2)2=22可知,它表示以(1,-2)为圆心,半径等于2的圆.
令x=1+2cosθ,y=-2+2sinθ,
则S=2x+y=2+4cosθ-2+2sinθ=4cosθ+2sinθ.
∴|S|≤ =2
=2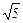 ,
,
即-2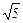 ≤S≤2
≤S≤2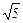 .
.
∴S的最大值是2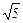 ,最小值为-2
,最小值为-2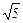 .
.