问题
解答题
如图,在Rt△ABC中,AB=AC,BD平分∠ABC,请你猜想线段AB、AD、BC之间的数量关系,并证明你猜想的正确性.(证明你的猜想需要用题中所有条件)
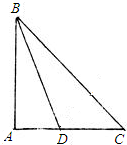
答案
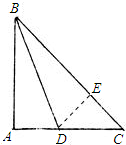
证明:AB+AD=BC,证明如下:
过点D作DE⊥BC,垂足为E,
∵BD平分∠ABC,
∴DA=DE,∠ABD=∠EBD(角平分线上的任一点到角的两条边的距离相等),
∵BD=BD,
∴△ABD≌△EBD,
∴AB=BE,
∴∠A=∠BED=90°,
∵AB=AC,
∴∠B=∠C=45°.
在△DEC中,∠DEC=90°,∠C=45°,
∴∠EDC=45°,
∴ED=EC,
∴AD=EC,
∴BE+EC=AB+AD=BC.
