如图所示,倾角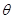 =30°。的光滑斜面MN底端固定一轻弹簧,轻弹簧的上端与滑块A固定连接,弹簧劲度系数k-100N/m,A静止且与距斜面顶端N点相距x=0.10m。另一小滑块B在N点以初速度
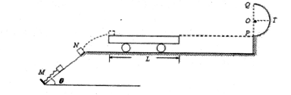
=30°。的光滑斜面MN底端固定一轻弹簧,轻弹簧的上端与滑块A固定连接,弹簧劲度系数k-100N/m,A静止且与距斜面顶端N点相距x=0.10m。另一小滑块B在N点以初速度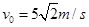 沿斜面向下运动,A、B碰撞后具有相同速度但不粘连。B与A分离后,B恰水平进入停放在光滑水平地面上的小车最左端,小车右端与墙壁足够远,小车上表面与半圆轨道最低点P的切线相平,小车与墙壁碰撞时即被粘在墙壁上。已知水平地面和半圆轨道面均光滑,滑块A、B可视为质点且质量均为m=2kg,被A压缩时弹簧存储的弹性势能Ep=0.5J,小车质量M=lkg、长L=l.0m,滑块B与小车上表面间的动摩擦因数
沿斜面向下运动,A、B碰撞后具有相同速度但不粘连。B与A分离后,B恰水平进入停放在光滑水平地面上的小车最左端,小车右端与墙壁足够远,小车上表面与半圆轨道最低点P的切线相平,小车与墙壁碰撞时即被粘在墙壁上。已知水平地面和半圆轨道面均光滑,滑块A、B可视为质点且质量均为m=2kg,被A压缩时弹簧存储的弹性势能Ep=0.5J,小车质量M=lkg、长L=l.0m,滑块B与小车上表面间的动摩擦因数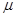 =0.2,g取l0m/s2。求:
=0.2,g取l0m/s2。求:
(I)滑块B与A碰撞结束瞬间的速度;
(2)小车与墙壁碰撞前瞬间的速度;
(3)为使滑块B能沿圆轨道运动而不脱离圆轨道,对轨道半径R有何要求?
(1) ;(2)
;(2) ;(3)
;(3) 或
或
题目分析:(1)设碰撞前瞬间,B的速度为 ,从释放B到与A撞前,由动能定理:
,从释放B到与A撞前,由动能定理:

解得:
设撞后B的速度为 ,对B、A碰撞过程
,对B、A碰撞过程
由动量守恒定律可得:
联立得: 5分
5分
(2)刚开始滑块A处于平衡状态,设此时弹簧压缩量为 ,对A受力分析可得:
,对A受力分析可得:

解得:
因 
弹簧恢复原长时,上端的位置恰好在N点,B、A碰撞后,保持整体直至弹簧恢复原长时在N点分离。
设即将分离时A、B的速度为 ,从A、B碰后开除以A、B即将分离,由动量守恒:
,从A、B碰后开除以A、B即将分离,由动量守恒:

解得:
此后B从斜面飞出做斜抛运动直至最高点,设其落入小车最左端速度大小为 ,
,
则:
设小车的滑块共同速度为 ,
,
滑块与小车相对运动过程中动量守恒:
代入数据解得:
以滑块与小车的相对位移为L1,由动量守恒定律

代入数据解得:
因小车左端距离墙壁足够远,则与墙壁碰撞前,滑块与小车具有共同的速度
故小车与墙壁碰撞时的速度 10分
10分
(3)小车撞墙后,滑块将在小车上继续向右做匀速度为 ,
,
位移为 的匀减速运动,然后滑上圆轨道的最低点P。
的匀减速运动,然后滑上圆轨道的最低点P。
若滑块恰能滑上圆轨道的最高点Q,设此时的速度为v,
临界条件:
根据动能定理有
联立并代入数据得:
若滑块恰好滑至 圆弧到达T点时速度减为0,则滑块也能沿圆弧轨道运动而不脱离轨道。
圆弧到达T点时速度减为0,则滑块也能沿圆弧轨道运动而不脱离轨道。
根据动能理:
代入数据得:
综上力述,滑块能沿圆轨道运动而不脱离圆轨道的半径
必须满足 或
或 5分
5分
