问题
计算题
如图所示，水平面上有两根相距0.5m的足够长的光滑平行金属导轨MN和PQ，它们的电阻可忽略不计，在M和P之间接有阻值为R="3.0Ω" 的定值电阻，导体棒ab长l=0.5m，质量m=1kg，其电阻为r=1.0Ω，与导轨接触良好.整个装置处于方向竖直向上的匀强磁场中，磁感应强度B=0.4T.现使ab 以v0="10m/s" 的速度向右做匀速运动.
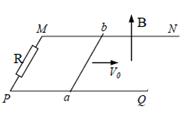
（1）使a、ｂ棒向右匀速的拉力F为多少？
（2）若撤掉拉力F，当导体棒速度v＝5m/s 时，试求导体棒的加速度大小为多少？
（3）试求从撤掉拉力F后，直至导体棒ab停止的过程中，在电阻R上消耗的焦耳热。
答案
（1）
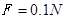；（2）
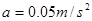；（3）37.5J
题目分析: （1）以
杆为研究对象，受力分析如图所示：
，解得：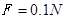
（2）由牛顿第二定律得：
又：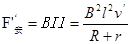
解得：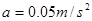
（3）根据功能原理知，导体棒动能的减少转化为全电路电阻消耗的电能，即：
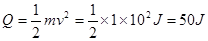
据回路电阻上能量消耗的关系可以得出在电阻R上消耗的焦耳热
QR=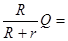
37.5J