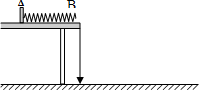
如图所示,将轻弹簧放在光滑的水平轨道上,一端与轨道的A端固定在一起,另一端正好在轨道的B端处,轨道固定在水平桌面的边缘上,桌边悬一重锤.利用该装置可以找出弹簧压缩时具有的弹性势能与压缩量之间的关系.
(1)为完成实验,还需下列哪些器材?答:______.
A.秒表 B.刻度尺 C.白纸 D.复写纸 E.小球 F.游标卡尺
(2)如果在实验中,得到弹簧压缩量x和小球离开桌面后的水平位移s的一些数据如下表,则得到的实验结论是______.
| 实验次序 | 1 | 2 | 3 | 4 |
| x/cm | 2.00 | 3.00 | 4.00 | 5.00 |
| s/cm | 10.20 | 15.14 | 20.10 | 25.30 |
(1)弹簧释放后,小球在弹簧的弹力作用下加速,弹簧与小球系统机械能守恒,小球离开桌面后,做平抛运动,根据平抛运动的知识可以求平抛的初速度,从实验数据得出弹簧的压缩量与小球的射程的关系,再从前面的结论得到弹性势能与小球的射程的关系,最后综合出弹簧的弹性势能EP与弹簧长度的压缩量x之间的关系.所以该实验中需要的器材有:B.刻度尺,用来测量弹簧压缩量x和小球离开桌面后的水平位移s
C.白纸,D.复写纸,E.小球,小球平抛后落在放有复写纸的白纸上,确定落地的位置.
故选BCDE.
(2)释放弹簧后,弹簧储存的弹性势能转化为小球的动能
Ep=
mv2 ①1 2
小球接下来做平抛运动,有
s=vt ②
h=
gt2 ③1 2
由①②③式可解得
Ep=
④ms2g 4h
由④的结论知:EP∝s2,
题目表格中给定的数据可知s∝x,综上可知:EP∝s2
故弹簧的弹性势能EP与弹簧长度的压缩量x之间的关系为EP∝x2,即 弹簧的弹性势能与弹簧压缩量的平方成正比.
故答案为:(1)BCDE
(2)弹簧的弹性势能与弹簧压缩量的平方成正比
