问题
解答题
已知函数f(x)=sinx+
(I)求f(x)的周期和振幅; (II)用五点作图法作出f(x)在一个周期内的图象; (III)写出函数f(x)的递减区间. |
答案
(I)y=2(
sinx+1 2
cosx)=2(sinxcos3 2
+cosxsinπ 3
)π 3
=2sin(x+
)(2分)π 3
∴函数f(x)的周期为T=2π,振幅为2.(4分)
(II)列表:
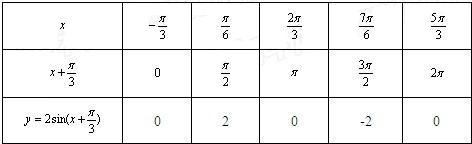
(7分)
图象如图.
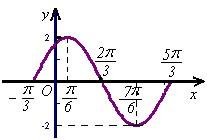
(9分)
(III)由2kπ+
≤x+π 2
≤2kπ+π 3
(k∈Z)解得:(10分)3π 2
2kπ+
≤x≤2kπ+π 6
(k∈Z)7π 6
所以函数的递减区间为[2kπ+
,2kπ+π 6
](k∈Z)(12分)7π 6
