问题
解答题
已知圆C:(x-2)2+(y-1)2=1,求过A(3,4)的圆C的切线方程.
答案
4x-3y=0,x=3
设过A(3,4)的直线y-4=k(x-3),即kx-y+4-3k=0
 由
由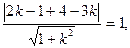 得k=
得k=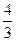
∴切线方程为 ,即4x-3y=0
,即4x-3y=0
但过A(3,4)向圆可作两条切线,一条从斜率不存在的直线中去找,一条切线为x=3
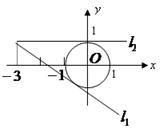
已知圆C:(x-2)2+(y-1)2=1,求过A(3,4)的圆C的切线方程.
4x-3y=0,x=3
设过A(3,4)的直线y-4=k(x-3),即kx-y+4-3k=0
 由
由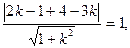 得k=
得k=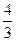
∴切线方程为 ,即4x-3y=0
,即4x-3y=0
但过A(3,4)向圆可作两条切线,一条从斜率不存在的直线中去找,一条切线为x=3
