问题
解答题
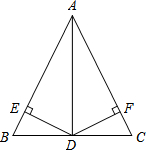
已知：如图，在△ABC中，AD是它的角平分线，且EB=FC，DE⊥AB，DF⊥AC，垂足分别为E，F．求证：BD=CD．
答案
证明：∵AD是△ABC的角平分线，DE⊥AB，DF⊥AC，
∴DE=DF，
在△BDE和△CDF中，
，EB=FC ∠BED=∠CFD=90° DE=DF
∴△BDE≌△CDF（SAS），
∴BD=CD．
搜题请搜索小程序“爱下问搜题”
已知：如图，在△ABC中，AD是它的角平分线，且EB=FC，DE⊥AB，DF⊥AC，垂足分别为E，F．求证：BD=CD．
证明：∵AD是△ABC的角平分线，DE⊥AB，DF⊥AC，
∴DE=DF，
在△BDE和△CDF中，
，EB=FC ∠BED=∠CFD=90° DE=DF
∴△BDE≌△CDF（SAS），
∴BD=CD．