二次函数y=ax2+bx+c过点A、B两点(A左B右),且分布在y轴两侧,且OA、OB的长是方程x2-5x+4=0的两根,且OA>OB,与y轴交于点C(0,4).
(1)求4a-2b+c的值;
(2)连接AC、BC,P是线段AB上一动点,且AP=m,过点P作PM∥AC,交BC于M,当m为何值时,S△PCM的面积最大,并求出这个最大值;
(3)△ABC外接圆的面积是______.(直接写出答案,结果保留π)
(1)∵OA、OB的长是方程x2-5x+4=0的两根,且OA>OB,
∴OA=4,OB=1,
∵二次函数y=ax2+bx+c过点A、B两点(A左B右),且分布在y轴两侧,
∴A(-4,0),B(1,0),设抛物线的解析式是y=a(x-1)(x+4),
把C(0,4)代入得:4=a(0-1)(0+4),
a=-1,
∴y=-(x-1)(x+4)=-x2-3x+4,
4a-2b+c=4×(-1)-2×(-3)+4=6,
答:4a-2b+c的值是6;
(2)∵AP=m,
∴PB=5-m,
∵PM∥AC,
∴△PBM∽△ABC,
∴
=(S△PBM S△ABC
)2,5-m 5
又∵S△ABC=10,
∴S△PBM=
,2(m-5)2 5
又∵S△PCB=2(5-m),
∴S△PCM=10-2m-
=-2(m-5)2 5
(m-2 5
)2+5 2
,5 2
∴当m=
时,△PCM的面积最大,最大值是5 2
,5 2
答:当m为
时,S△PCM的面积最大,这个最大值是5 2
.5 2
(3)故答案为:
π.17 2

 Si(粗)+2CO↑ ②Si(粗)+3HCl
Si(粗)+2CO↑ ②Si(粗)+3HCl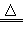 SiHCl3+H2 ③SiHCl3+H2
SiHCl3+H2 ③SiHCl3+H2 Si(纯)+3HCl。下列说法错误的是 [ ]
Si(纯)+3HCl。下列说法错误的是 [ ]