问题
计算题
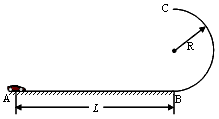
某校物理兴趣小组决定举行遥控赛车比赛,比赛路径如图所示。可视为质点的赛车从起点A出发,沿水平直线轨道运动L后,由B点进入半径为R的光滑竖直半圆轨道,并通过半圆轨道的最高点C,才算完成比赛。B是半圆轨道的最低点,水平直线轨道和半圆轨道相切于B点。已知赛车质量m=0.5 kg,通电后以额定功率P=2 W工作,进入竖直圆轨道前受到的阻力恒为Ff=0.4 N,随后在运动中受到的阻力均可不计,L=10.00 m,R=0.32 m。求:(g取10 m/s2)
(1)要使赛车完成比赛,赛车在半圆轨道的B点对轨道的压力至少多大;
(2)要使赛车完成比赛,电动机至少工作多长时间;
(3)若电动机工作时间为t0=5s,当R为多少时赛车既能完成比赛且飞出的水平距离又最大,水平距离最大是多少?
答案
解:(1)当赛车恰好过C点时在B点对轨道压力最小,赛车在B点对有:
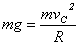
解得 ①
①
对赛车从B到C由机械能守恒定理得: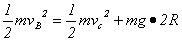 ②
②
对赛车在B处受力分析,则: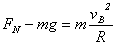 ③
③
由①②③得: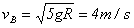 ,
, 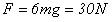
(2)对赛车从A到B由动能定理得: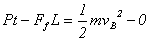
解得:t=2s
(3)对赛车从A到C由动能定理得: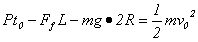
赛车飞出C后有: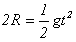 ,
,
解得: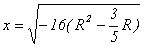
所以,当R=0.3m时x最大,xmax=1.2m
