问题
解答题
求圆心在直线y＝－2x上，并且经过点A(2,－1)，与直线x＋y＝1相切的圆的方程.
答案
圆的方程为：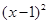
＋
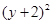＝2
利用圆心和半径表示圆的方程，首先
设圆心为S，则KSA＝1,∴SA的方程为：y＋1＝x－2，即y＝x－3， ………4分
和y＝－2x联立解得x＝1,y＝－2，即圆心(1,－2)
∴r＝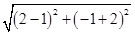
＝
,
故所求圆的方程为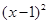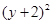：＋＝2
解：法一：
设圆心为S，则KSA＝1,∴SA的方程为：y＋1＝x－2，即y＝x－3， ………4分
和y＝－2x联立解得x＝1,y＝－2，即圆心(1,－2) ……………………8分
∴r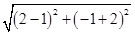＝＝, ………………………10分
故所求圆的方程为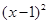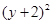：＋＝2 ………………………12分
法二：由条件设所求圆的方程为：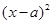
＋
＝
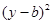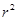
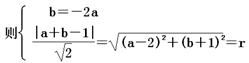, ………………………6分
解得a＝1,b＝－2,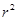＝2 ………………………10分
所求圆的方程为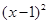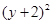：＋＝2 ………………………12分
其它方法相应给分