问题
解答题
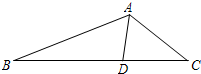
如图,在△ABC中,AD是∠BAC的角平分线,AB=3,AC=2,∠BAC=120°,求
 |
答案
过点C作CE⊥BA交BA延长线于点E,过点D作DF⊥AB于F,DG⊥AC于G,
∵AB=3,AC=2,∠BAC=120°,
∴∠EAC=60°,
∴AE=AC•cos∠EAC=2×
=1,EC=AC•sin∠EAC=2×1 2
=3 2
,3
∴S△ABC=
AB•EC=1 2
×3×1 2
=3
,3 3 2
∵AD是∠BAC的角平分线,
∴DF=DG,∠FAD=
∠BAC=60°,1 2
∴S△ABC=
AB•DF+1 2
AC•DG=1 2
DF(AB+AC)=1 2
×DF×(2+3)=1 2
,3 3 2
∴DF=
,3 3 5
∴在Rt△ADF中,AD=
=DF sin∠FAD
=3 3 5 3 2
,6 5
∴
=AD AB
=6 5 3
.2 5

