问题
选择题
如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,DE是斜边AB的垂直平分线,且DE=1cm,则AC长为( )
A.2.5cm
B.3cm
C.3.5cm
D.4cm
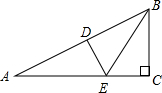
答案
∵BE平分∠ABC,ED⊥BA,EC⊥BC,
∴ED=EC=1cm,又BE=BE,
∴Rt△BDE≌Rt△BCE(HL),
∴BD=BC,
又∵DE垂直平分AB,
∴AE=BE,AD=BD,
设AE=BE=xcm,则有AC=(x+1)cm,
在Rt△ADE中,根据勾股定理得:AD2+DE2=AE2,
∴AD=BC=
cm,AB=2AD=2x2-1
cm,x2-1
在Rt△ABC中,根据勾股定理得:AB2=AC2+BC2,
即4(x2-1)=(x+1)2+x2-1,
整理得:(x-2)(x+1)=0,
解得:x=2或x=-1(舍去),
故AC=2+1=3cm.
故选B.
