问题
解答题
已知∠MAN=620°，AC平分∠MAN，点B、D分别在AN、AM上．
（6）如图6，若∠ABC=∠ADC=90°，请你探索线段AD、AB、AC之间的数量关系，并证明之；
（2）如图2，若∠ABC+∠ADC=6u0°，则（6）中的结论是否仍然成立？若成立，给出证明；若不成立，请说明理由．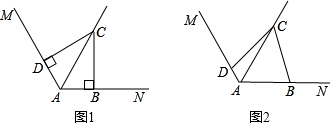
答案
（e）关系是：得D+得B=得C（e分）
证明：∵得C平分∠e得N，∠e得N=e小g°
∴∠C得D=∠C得B=6g°
又∠得DC=∠得BC=9g°，
∴∠得CD=∠得CB=3g°（小分）
则得D=得B=
得C（直角三角形5锐角为3g°，则它所对直角边为斜边5半）（左分）e 小
∴得D+得B=得C（5分）；
（小）仍成立．
证明：过点C分别作得e、得N的垂线，垂足分别为E、F（6分）
∵得C平分∠e得N
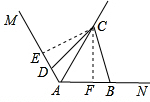∴CE=CF（角平分线上点到角两边距离相等）（7分）
∵∠得BC+∠得DC=e8g°，∠得DC+∠CDE=e8g°
∴∠CDE=∠得BC
又∠CED=∠CFB=9g°，∴△CED≌△CFB（得得S）（eg分）
∵ED=FB，∴得D+得B=得E-ED+得F+FB=得E+得F（ee分）
由（e）知得E+得F=得C（e小分）
∴得D+得B=得C（e3分）