搜题请搜索小程序“爱下问搜题”
问题 解答题
已知函数f(x)=sin(2x-
π
6
)
（Ⅰ）求函数y=f（x）的单调增区间；      
（Ⅱ）求函数f（x）在区间[-
π
12
，
π
2
]上的值域；
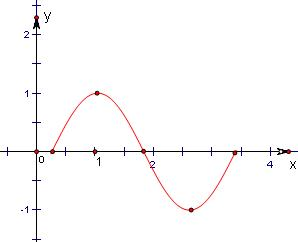
（Ⅲ）画出函数y=f（x）在一个周期上的简图．
答案

（I）令u=2x-

π
6
，则函数y=3sinu的单调增区间为[-
π
2
+2kπ，
π
2
+2kπ]k∈Z（5分）

由-

π
2
+2kπ≤2x-
π
6
≤
π
2
+2kπ，得：

-

π
6
+kπ≤x≤
π
3
+kπk∈Z

函数y=3sin（2x-

π
6
）的单调增区间为：[-
π
6
+kπ，
π
3
+kπ]k∈Z（8分）

（II）∵x∈[-

π
12
，
π
2
]，可得2x-
π
6
∈[-
π
3
，
5π
6
]

∴当2x-

π
6
=
π
2
，即x=
π
3
时，函数的取最大值为1

又∵f（-

π
12
）=-
3
2
＜f（
π
2
）=
1
2
，

∴当x=

π
12
时，函数取最小值-
3
2
，

综上所述，函数f（x）在区间[-

π
12
，
π
2
]上的值域为[-
3
2
，1]．

（III）根据题意列出表格得：

  t0  
π
2
 π  
3π
2
 2π
x
π
12
π
3
  
7π
12
  

5π
6
  

13π
12
y 01 0-1 0
简图：

单项选择题

李某与赵某是夫妻。2002年7月，李某向某县人民法院起诉要求离婚，法院经审理判决不准离婚。审理该案的书记员两次到李某家送达判决书李某均拒绝接收。对此，应当如何处理

A．书记员将该判决书交给李的邻居王某转交

B．书记员将该判决书留置李某的住所

C．书记员将该判决书交给李某所在地居委会转交

D．书记员将该判决书交给李某所在地派出所转交
查看答案
问答题

审稿题：审读短文，改正错误，弥补缺漏。（本题20分）出版工作由编辑、出版、发行三大环节组成，其中发行工作是中心环节。通过各种方式，将出版物向公众广泛发行，是出版活动的内在动机和目的。编辑过程可以按时间顺序的前后和工作内容的重点分成若干基本环节。这些基本环节主要包括信息采集、选题策划、组稿、审稿、签订出版合同、编辑加工整理、整体设计、审定发稿、排版、校样处理、印制、样品检查、出版物宣传、反馈信息收集等。编辑过程的各个环节之间的关系错综复杂又各自独立。其中，信息采集在编辑过程的各个环节中具有重要的地位。选题策划要以信息采集为基础，信息采集要以选题策划为中心。信息采集是组稿的依据，组稿是选题的落实和具体化。审稿和编辑加工整理的关系不是十分紧密，重要的稿件必须经过审稿环节才可以进入编辑加工整理环节，而一般的稿件无须经过审稿环节就可以直接进入编辑加工整理环节。审定发稿及其后续工作，如校样处理、样品检查等，也是编辑过程中不可或缺的环节。作为出版工作成果的出版物，具有物质产品和精神产品双重属性，而物质产品属性是其本质属性。
查看答案