(本小题满分12分)在平面直角坐标系xOy中,已知双曲线C1:2x2-y2=1.
(1)过C1的左顶点引C1的一条渐近线的平行线,求该直线与另一条渐近线及x轴围成的三角形的面积;
(2)设斜率为1的直线l交C1于P、Q两点.若l与圆x2+y2=1相切,求证:OP⊥OQ;
(1) S=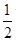 |OA||y|=
|OA||y|=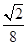 .(2)见解析。
.(2)见解析。
(1)先把双曲线的方程化成标准方程可求出a值,从而得到左顶点A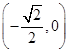 ,渐近线方程:y=±
,渐近线方程:y=±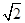 x,然后可设出过点A与渐近线y=
x,然后可设出过点A与渐近线y=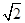 x平行的直线方程为y=
x平行的直线方程为y=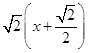 ,即y=
,即y=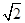 x+1.它再与另一条渐近线方程联立解方程组可求出交点坐标,从而得到所求三角形的高,度显然等于|OA|,面积得解.
x+1.它再与另一条渐近线方程联立解方程组可求出交点坐标,从而得到所求三角形的高,度显然等于|OA|,面积得解.
(2) 设直线PQ的方程是y=x+b,因直线PQ与已知圆相切,
故 =1,即b2=2.
=1,即b2=2.
由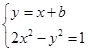 得x2-2bx-b2-1=0(*)
得x2-2bx-b2-1=0(*)
设P(x1,y1)、Q(x2,y2),然后证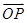 ·
·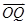 =x1x2+y1y2=x1x2+(x1+b)(x2+b)=2x1x2+b(x1+x2)+b2,借助(*)式方程中的韦达定理代入此式证明
=x1x2+y1y2=x1x2+(x1+b)(x2+b)=2x1x2+b(x1+x2)+b2,借助(*)式方程中的韦达定理代入此式证明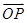 ·
·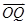 =0即可.
=0即可.
(1)双曲线C1: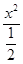 -y2=1,左顶点A
-y2=1,左顶点A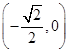 ,渐近线方程:y=±
,渐近线方程:y=±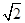 x.
x.
过点A与渐近线y=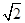 x平行的直线方程为y=
x平行的直线方程为y=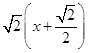 ,即y=
,即y=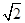 x+1.
x+1.
解方程组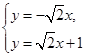 得
得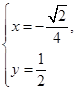
所以所求三角形的面积为S=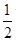 |OA||y|=
|OA||y|=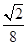 .
.
(2)设直线PQ的方程是y=x+b,因直线PQ与已知圆相切,
故 =1,即b2=2.
=1,即b2=2.
由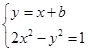 得x2-2bx-b2-1=0.
得x2-2bx-b2-1=0.
设P(x1,y1)、Q(x2,y2),则
又y1y2=(x1+b)(x2+b),所以
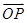 ·
·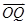 =x1x2+y1y2=2x1x2+b(x1+x2)+b2
=x1x2+y1y2=2x1x2+b(x1+x2)+b2
=2(-1-b2)+2b2+b2=b2-2=0.
故OP⊥OQ.

 的同时,降低
的同时,降低