问题
解答题
已知圆A：x2＋y2－2x－2y－2＝0.
(1)若直线l：ax＋by－4＝0平分圆A的周长，求原点O到直线l的距离的最大值；
(2)若圆B平分圆A的周长，圆心B在直线y＝2x上，求符合条件且半径最小的圆B的方程．
答案
（1）
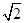（2）(x－
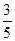)2＋(y－
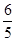)2＝
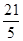
(1)圆A的方程即(x－1)2＋(y－1)2＝4，其圆心为A(1,1)，半径为r＝2.
由题意知直线l经过圆心A(1,1)，所以a＋b－4＝0，得b＝4－a.
原点O到直线l的距离d＝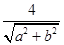
.
因为a2＋b2＝a2＋(4－a)2＝2(a－2)2＋8，所以当a＝2时，a2＋b2取得最小值8.
故d的最大值为
＝.
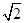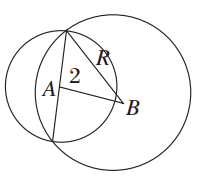
(2)由题意知圆B与圆A的相交弦为圆A的一条直径，它经过圆心A.
设圆B的圆心为B(a,2a)，半径为R.如图所示，在圆B中，
由垂径定理并结合图形可得：R2＝22＋|AB|2＝4＋(a－1)2＋(2a－1)2＝5(a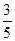－)2＋.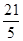
所以当a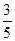＝时，R2取得最小值.
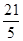故符合条件且半径最小的圆B的方程为(x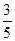－)2＋(y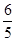－)2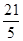＝.