问题
问答题
如图所示,半径为2m的光滑圆环竖直放置,A点为圆环的最低点,B为圆环的最高点,∠CBA小于5°,CDA为光滑斜面,CEA为光滑圆弧面.小球由静止开始分别从C点沿光滑斜面CDA和圆弧面CEA滑至A点,时间分别为t1、t2,试比较t1、t2的大小.
某同学的解题思路如下:
根据机械能守恒,由静止开始分别从C点沿光滑斜面CDA和沿圆弧CEA滑至A点的速度大小相等,而沿斜面CDA滑下的路程较短,所用时间也较短,所以t1<t2.
你认为该同学的解法正确吗?若正确,请计算出t1、t2的大小;若不正确,指出错误处并通过计算说明理由.
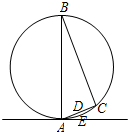
答案
不正确.
由于小球沿圆弧CEA运动不是匀变速运动,不能仅根据末速度大小和路程来比较t1与t2的大小.
正确设CDA斜面倾角为θ
则 2R sinθ=
gt121 2
解得t1=
=4R g
s=0.89s 4×2 10
物体沿圆弧CEA运动时,由于圆弧CEA对应的圆心角小于5°,所以小球的运动可以看成单摆的简谐振动,
所以有t2=
=T 4 π 2
=0.7s R g
所以 t1>t2
