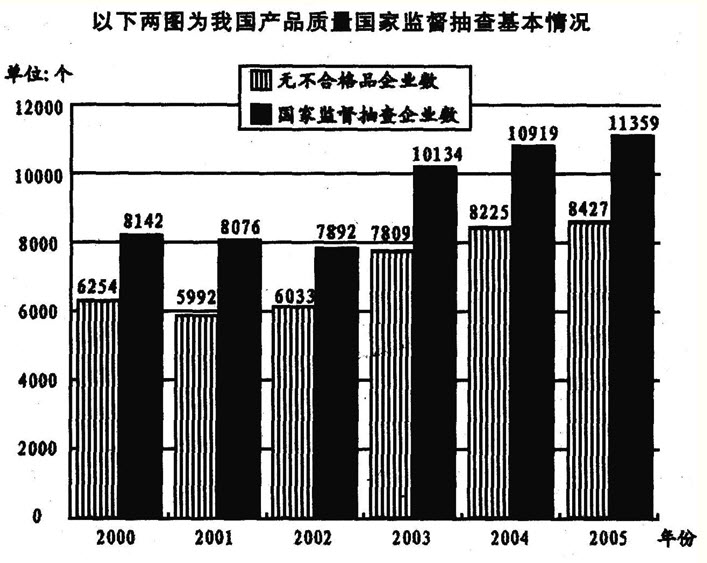
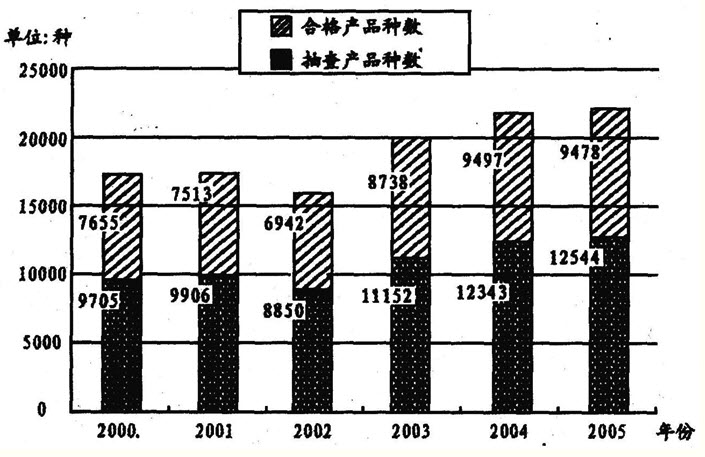
问题
解答题
设一动点M在x轴正半轴上,过动点M与定点P(1,2)的直线交y=x(x>0)于点Q,动点M在什么位置时,
|
答案
设l:y=k(x-2)+1,要它与y=x(x>0)相交,则k>1或k<0.
令y=0,得M(2-
,0),令y=x,得Q1 k
.
,&2k-1 k-1 2k-1 k-1
∴|MP|=
,1+k2 k2
= &|PQ|
.1+k2 (1-k)2
∴u=
+1 |PM|
=1 |PQ|
+|k| 1+k2
=|1-k| 1+k2
(k<0)1-2k 1+k2
(k>1)2k-1 1+k2
于是u2=
⇒(u2-4)k2+4k+u2-1=0.(1-2k)2 1+k2
由△≥0,得u2(u2-5)≤0,
∴0≤u2≤5
.,&∴u≤ 5
而当l的方程为x=2时,u=2,
∴umax=
对应得k=-2,进而求得M(5
,0).5 2