问题
填空题
圆x2+y2=20的弦AB的中点为P(2,-3)，则弦AB所在直线的方程是
答案
2x-3y-13=0
题目分析：设弦的端点为A（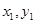
），B（
），代入圆的方程，两式相减并整理得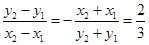
，由直线方程的点斜式得弦AB所在直线的方程是2x-3y-13=0。
点评：简单题，研究直线与圆的位置关系，涉及弦中点问题，可尝试利用“点差法”求弦的斜率。
搜题请搜索小程序“爱下问搜题”
圆x2+y2=20的弦AB的中点为P(2,-3)，则弦AB所在直线的方程是
2x-3y-13=0
题目分析：设弦的端点为A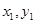（），B（），代入圆的方程，两式相减并整理得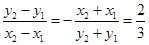，由直线方程的点斜式得弦AB所在直线的方程是2x-3y-13=0。
点评：简单题，研究直线与圆的位置关系，涉及弦中点问题，可尝试利用“点差法”求弦的斜率。