问题
解答题
已知t∈R,圆C:x2+y2-2tx-2t2y+4t-4=0.
(1)若圆C的圆心在直线x-y+2=0上,求圆C的方程;
(2)圆C是否过定点?如果过定点,求出定点的坐标;如果不过定点,说明理由.
答案
(1)x2+y2+2x-2y-8=0或x2+y2-4x-8y+4=0(2)过定点(2,0).
(1)配方得(x-t)2+(y-t2)2=t4+t2-4t+4,其圆心C(t,t2).依题意t-t2+2=0t=-1或2.
即x2+y2+2x-2y-8=0或x2+y2-4x-8y+4=0为所求方程.
(2)整理圆C的方程为(x2+y2-4)+(-2x+4)t+(-2y)·t2=0,令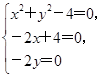
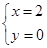
故圆C过定点(2,0).
