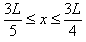问题
计算题
如图所示，质量为m的小球，由长为L的细线系住，细线的另一端固定在A点，AB是过A点的竖直线，在AB线上钉铁钉D，若线能承受的最大拉力为9mg，现将小球拉直成水平，然后静止释放，小球能绕钉子在竖直平面内做完整的圆周运动，求钉子位置到A点距离的取值范围。（不计线与钉子碰撞时的能量损失）
答案
解：设铁钉D距A点距离为x，当绳子拉力最大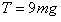
时，小球从最高点到最低点机械能守恒：
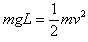
对小球在最低点，由牛顿第二定律：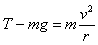
又因：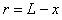
联立以上得：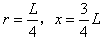
小球绕D点做圆周运动到最高点有：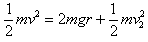
由以上可得：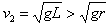
，能做完整圆周运动
若小球绕D点刚好能做完整圆周运动，则从初始位置到最高有：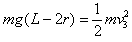
又因：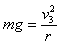
联立以上得：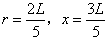
综合可得：