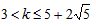问题
计算题
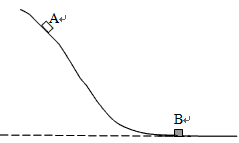
一质量为m的小滑块A沿斜坡由静止开始下滑,与一质量为km的静止在水平地面上的小滑块B发生正碰撞,如图所示。设碰撞是弹性的,且一切摩擦不计。为使二者能且只能发生两次碰撞,则k的值应满足什么条件?
答案
解:设A与B碰撞前A的速度为v0,碰后A与B的速度分别为v1与V1,由动量守恒及机械能守恒定律有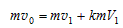 ①
①
 ②
②
由此解得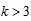 ③ ,
③ , 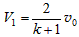 ④
④
为使A能回到坡上,要求v1<0,这导致k>1;为使A从坡上滑下后再能追上B,应有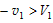 ,即
,即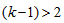 ,这导致
,这导致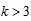 ,于是,为使第二次碰撞能发生,要求 k > 3 ⑤
,于是,为使第二次碰撞能发生,要求 k > 3 ⑤
对于第二次碰撞,令v2和V2分别表示碰后A和B的速度,同样由动量守恒及机械能守恒定律有: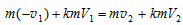 ,
,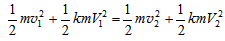
由此解得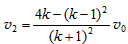 ⑥ ,
⑥ , 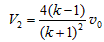 ⑦
⑦
若v2>0,则一定不会发生第三次碰撞,若v2<0,且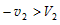 ,则会发生第三次碰撞。
,则会发生第三次碰撞。
故为使第三次碰撞不会发生,要求A第三次从坡上滑下后速度的大小不大于B速度的大小,即
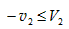 ⑧
⑧
由⑥⑦⑧式得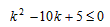 ⑨
⑨
由 k2-10 k + 5 =0 可求得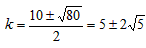
⑨式的解为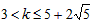 ⑩
⑩
⑩与⑤的交集即为所求: