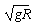问题
计算题
如图所示，长为R的轻绳，上端固定在O点，下端连一小球。小球接近地面，处于静止状态。现给小球一沿水平方向的初速度v0，小球开始在竖直平面内做圆周运动。设小球到达最高点时绳突然断开。已知小球最后落在离小球最初位置2R的地面上。求：
（1）小球在最高点的速度v；
（2）小球的初速度v0；
（3）小球在最低点时球对绳的拉力；
（4）如果细绳转过60°角时突然断开，则小球上升到最高点时的速度多大？（小球的质量为m，重力加速度为g）。
答案
解：（1）在水平方向有2R＝vt
在竖直方向有2R＝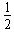
gt2
解得v＝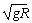
（2）根据机械能守恒定律有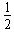
mv02－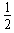
mv2＝mg2R
解得v0＝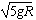
（3）对小球分析有F－mg＝m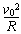
解得F＝6mg
由牛顿第三定律可知：小球对绳子的拉力为6mg，方向向下
（4）设绳断时的速度为v1，有mgR（1－cos60°）＝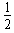
mv02－
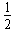mv12
设小球在最高点时的速度为v2，有v2＝v1cos60°
v2＝