问题
计算题
如图所示半径为R、r(R>r)甲、乙两圆形轨道安置在同一竖直平面内,两轨道之间由一条水平轨道(CD)相连,如小球从离地3R的高处A点由静止释放,可以滑过甲轨道,经过CD段又滑上乙轨道后离开两圆形轨道,小球与CD段间的动摩擦因数为μ,其余各段均光滑。
(1)求小球经过甲圆形轨道的最高点时小球的速度?
(2)为避免出现小球脱离圆形轨道而发生撞轨现象,试设计CD段的长度。

答案
解:(1)设小球能通过甲轨道最高点时速度为v1
由机械能守恒定律得: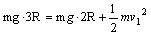
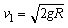
(2)小球在甲轨道上做圆周运动通过最高点的最小速度为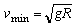
∵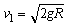 >
>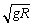
∴小球能通过甲轨道而不撞轨
设CD的长度为x,小球在乙轨道最高点的最小速度为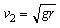
小球要通过乙轨道最高点,则需满足: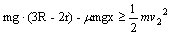
得:x≤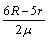
小球到乙轨圆心等高处之前再返回,则需满足: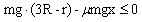 且
且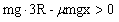
得: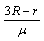 ≤x<
≤x<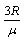
总结论:CD≤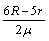 或
或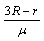 ≤CD <
≤CD <