问题
计算题
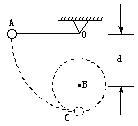
小球A用不可伸长的轻绳悬于O点,在O点的正下方有一固定的钉子B,OB=d,如图所示。开始时,小球与O在同一水平面处无初速释放,绳长为L。不计轻绳与钉子碰撞时的能量损失,为使球能绕B点做圆周运动,试求d的取值范围。
答案
解:由圆周运动的知识可知,当小球以B点为圆心做圆周运动时,到达最高点时向心力由重力提供时速度最小。即mg=m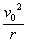 =m
=m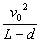
v0=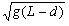
取v0所在处的平面为零势能面,对小球由开始运动到v0所在处运用机械能守恒定律可得mg(L-2r)= mv02
mv02
又r=L-d
联立方程可解得距离d=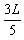
我们不难得到:小球做圆周运动的轨道半径越小,即d越大,小球越容易通过圆周的最高点。综合上述分析,距离d的值范围应为:L>d≥3L/5
