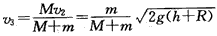问题
计算题
如图所示放在水平面上的小车上表面水平，AB是半径为R的1/4光滑圆弧轨道，下端B的切线水平且与平板车上表面平齐，车的质量为M。现有一质量为m的小滑块，从轨道上端A处无初速释放，滑到B端后，再滑到平板车上。若车固定不动，小滑块恰不能从车上掉下。（重力加速度为g）
（1）求滑块到达B端之前瞬间所受支持力的大小；
（2）求滑块在车上滑动的过程中，克服摩擦力做的功；
（3）若车不固定，且地面光滑，把滑块从A点正上方的P点无初速释放，P点到A点的高度为h，滑块从A点进入轨道，最后恰停在车的中点，求车的最大速度。
答案
解：（1）根据机械能守恒有：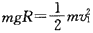
①
根据牛顿第二定律有：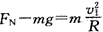
②
联立①②两式，得轨道对滑块的支持力：FN=3mg ③
（2）滑块在车上滑动过程中，克服摩擦力做的功W=mgR ④
（3）方法一：因滑块最后恰停在车的中点，所以因摩擦而产生的内能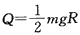
⑤
滑块与车速度相同时，车速最大，设为v2，根据能量守恒有：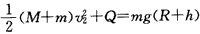
⑥
联立⑤⑥解得：
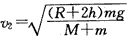⑦
方法二：滑块到B点速度为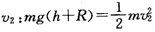
滑块最后恰停在车的中点时，滑块与车速度相同，车速最大，设为v3
mv2=(M+m)v3
解得：