问题
填空题
已知圆O:x2+y2=4,则过点P(2,4)与圆O相切的切线方程为________________.
答案
3x-4y+10=0或x=2
∵点P(2,4)不在圆O上,∴切线PT的直线方程可设为y=k(x-2)+4.根据d=r,∴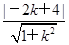 =2,解得k=
=2,解得k=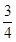 ,所以y=
,所以y=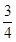 (x-2)+4,即3x-4y+10=0.因为过圆外一点作圆的切线应该有两条,可见另一条直线的斜率不存在.易求另一条切线为x=2.
(x-2)+4,即3x-4y+10=0.因为过圆外一点作圆的切线应该有两条,可见另一条直线的斜率不存在.易求另一条切线为x=2.
已知圆O:x2+y2=4,则过点P(2,4)与圆O相切的切线方程为________________.
3x-4y+10=0或x=2
∵点P(2,4)不在圆O上,∴切线PT的直线方程可设为y=k(x-2)+4.根据d=r,∴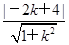 =2,解得k=
=2,解得k=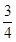 ,所以y=
,所以y=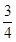 (x-2)+4,即3x-4y+10=0.因为过圆外一点作圆的切线应该有两条,可见另一条直线的斜率不存在.易求另一条切线为x=2.
(x-2)+4,即3x-4y+10=0.因为过圆外一点作圆的切线应该有两条,可见另一条直线的斜率不存在.易求另一条切线为x=2.