问题
计算题
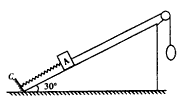
如图所示,在倾角为30°的光滑斜面上,一劲度系数为k的轻质弹簧一端固定在固定挡板C上,另一端连接一质量为m的物体A,一轻细绳通过定滑轮,一端系在物体A上,另一端有一细绳套,细绳与斜面平行,物体A处于静止状态。现在细绳套上轻轻挂上一个质量也为m的物体B,A将在斜面上做简谐运动。试求:
(1)物体A的最大速度值。
(2)物体B下降到最低点时,细绳对物体B的拉力值。
答案
解:(1)未挂物体B时,设弹簧压缩量为 ,对于物体A由平衡条件有:
,对于物体A由平衡条件有: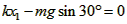
解得: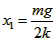 ①
①
挂B后A沿斜面向上做加速度减小的加速运动,当A加速度为0时,A速度最大,设此时弹簧伸长量为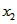 ,对于A由平衡条件有:
,对于A由平衡条件有: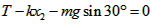 ②
②
当A加速度为0时,B加速度也为0,对于B由平衡条件: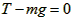 ③
③
由②③解得: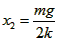
因x1与x2相等,故在此过程中弹簧弹性势能改变量ΔE=0 ④
设最大速度为v,对于A、B及弹簧组成的系统由机械能守恒得: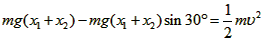 ⑤
⑤
将x1、x2代入⑤得: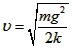
(2)A做简谐运动的振幅为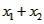 ,A运动到最高点时弹簧的伸长量
,A运动到最高点时弹簧的伸长量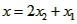
A在最高点时,由牛顿第二定律: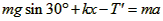
B在最低点时,由牛顿第二定律: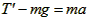
解得: 。
。
