问题
计算题
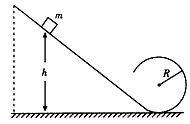
某游乐场过山车模型简化为如图所示，光滑的过山车轨道位于竖直平面内，该轨道由一段斜轨道和与之相切的圆形轨道连接而成，圆形轨道的半径为R。可视为质点的过山车从斜轨道上某处由静止开始下滑，然后沿圆形轨道运动。
（1）若要求过山车能通过圆形轨道最高点，则过山车初始位置相对于圆形轨道底部的高度至少要多少？
（2）考虑到游客的安全，要求全过程游客受到的支持力不超过自身重力的7倍，过山车初始位置相对于圆形轨道底部的高度不得超过多少？
答案
解：（1）设过山车总质量为M，从高度h1处开始下滑，恰能以v1过圆周轨道最高点，
在圆周轨道最高点有：
①
运动过程机械能守恒：
②
由①②式得：h1=2.5R
过山车初始位置相对圆形轨道底部的高度至少要2.5R
（2）设从高度h2处开始下滑，过圆周最低点时速度为v3，
游客受到的支持力最大是FN=7mg，
最低点时：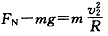
，运动过程机械能守恒：
④
由③④式得：h2=3R
过山车初始位置相对圆形轨道底部的高度不得超过3R。