问题
计算题
如图所示，质量为m的小球与一根不可伸长的长为L的轻绳相连接，绳的另一端固定于O点，现将小球拉到跟水平方向成30°角的上方（绳恰好伸直），然后将小球自由释放，求小球到最低点时受到绳子的拉力的大小。
答案
解：小球释放后，先做自由落体运动直到绳子绷直，根据对称性和三角形的全等关系，当绳子再次与水平方向的夹角为30°时，绳子与O点的距离再次为L，这时绳子刚好绷直，设绳刚绷直时获得的速度是v，则有
mg·2Lsin30°=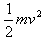
由于绳子绷紧瞬间，绳对球的作用力远大于球的重力，使小球沿绳子方向的速度突变为零，而小球在垂直于绳子方向的速度为v1不变，如图所示，则
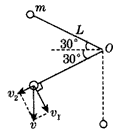
v1=vcos30°=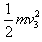
小球绷紧细绳后继续下摆到最低点的过程，机械能守恒
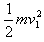+mgL(1-sin30°)=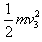
由向心力来源得FT-mg=m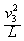
最低点绳子拉力FT=3.5mg
