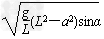问题
计算题
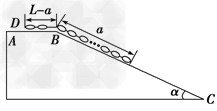
如图所示，AB为光滑的水平面，BC是倾角为α的足够长的光滑斜面(斜面体固定不动)。AB、BC间用一小段光滑圆弧轨道相连。一条长为L的均匀柔软链条开始时静止地放在ABC面上，其一端D至B的距离为L－a，现自由释放链条，则：
(1)链条下滑过程中，系统的机械能是否守恒？简述理由；
(2)链条的D端滑到B点时，链条的速率为多大？
答案
解：(1)链条机械能守恒，因为斜面是光滑的，只有重力做功，符合机械能守恒的条件
(2)设链条质量为m，始、末状态的重力势能变化可认为是由L－a段下降高度h引起的(如图所示)，即：
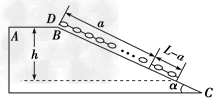
h＝(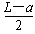
＋a)sinα＝
sinα
而该部分的质量为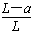：m'＝
m
即重力
势能变化量为：△Ep＝m'gh＝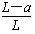
mg
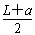sinα＝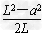
mgsinα
因为软链条的初速度为零，所以有：△Ek＝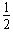
mv2
由机械能守恒定律△Ep＝△Ek
得：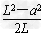
mgsinα＝
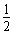mv2
所以v＝