问题
计算题
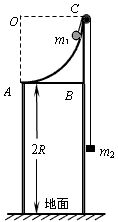
如图,半径为R的1/4圆弧支架竖直放置,支架底AB离地的距离为2R,圆弧边缘C处有一小定滑轮,一轻绳两端系着质量分别为m1与m2的物体,挂在定滑轮两边,且m1>m2,开始时m1、m2均静止,且m1在图示中的最高点紧贴圆弧边缘,m1、m2可视为质点,不计一切摩擦。求:
(1)m1释放后经过圆弧最低点A时的速度;
(2)若m1到最低点时绳突然断开,求m1落地点离A点水平距离;
(3)为使m1能到达A点,m1与m2之间必须满足什么关系?
答案
解:(1)设m1运动到最低点时速度为v1,此时m2的速度为v2,分解速度,得:v2=v1sin45°
由m1与m2组成系统,机械能守恒,有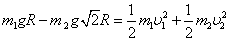
由上述两式求得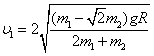
(2)断绳后m1做平抛运动,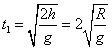
又s=v1t
由以上两式得s=4R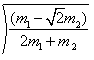
(3)m1能到达A点满足条件v1≥0
又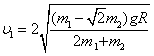
解得