问题
计算题
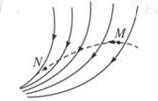
如图甲所示，竖直平面内的光滑轨道由直轨道AB和圆轨道BC组成，小球从轨道AB上高H处的某点由静止滑下，用力传感器测出小球经过圆轨道最高点C时对轨道的压力为F，并得到如图乙所示的压力F随高度H的变化关系图象．(小球在轨道连接处无机械能损失，g＝10 m/s2)求：
(1)小球从H＝3R处滑下，它经过最低点B时的向心加速度的大小；
(2)小球的质量和圆轨道的半径．
答案
解：(1)由机械能守恒得：mgH＝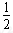
mvB2
向心加速度a＝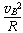
＝6g＝60 m/s2
(2)由机械能守恒得：mgH－mg2R＝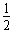
mvC2
由牛顿第二定律得：mg＋F＝m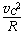
解得：F＝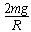
H－5mg
根据图象代入数据得：m＝0.1 kg，R＝0.2 m