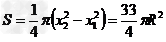如图为某种鱼饵自动投放器中的投饵管装置示意图,其下半部AB 是一长为2R 的竖直细管,上半部BC 是半径为R 的四分之一圆弧弯管,管口沿水平方向,AB 管内有一原长为R 、下端固定的轻质弹簧。投饵时,每次总将弹簧长度压缩到0.5R 后锁定,在弹簧上端放置一粒鱼饵,解除锁定,弹簧可将鱼饵弹射出去。设质量为m 的鱼饵到达管口C 时,对管壁的作用力恰好为零。不计鱼饵在运动过程中的机械能损失,且锁定和解除锁定时,均不改变弹簧的弹性势能。已知重力加速度为g 。求:
(1 )质量为m 的鱼饵到达管口C 时的速度大小V1;
(2) 弹簧压缩到0.5R时的弹性势能EP;
(3) 已知地面与水面相距1.5R,若使该投饵管绕AB管的中轴线OO′在90°角的范围内来回缓慢转动,每次弹射时只放置一粒鱼饵,鱼饵的质量在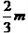 到m之间变化,且均能落到水面。持续投放足够长时间后,鱼饵能够落到水面的最大面积S是多少?
到m之间变化,且均能落到水面。持续投放足够长时间后,鱼饵能够落到水面的最大面积S是多少?
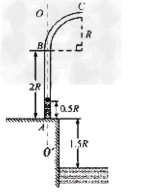
(1 )质量为m的鱼饵到达管口C时做圆周运动的向心力完全由重力提供,
则由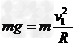
得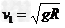
(2)弹簧的弹性势能全部转化为鱼饵的机械能,由机械能守恒定律有
联立方程解得Ep=3mgR
(3)鱼饵离开管口C作平抛运动,
则有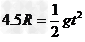
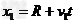
联立方程解得
当鱼饵质量为 时,设其到达管口的速度为v2,由机械能守恒定律有
时,设其到达管口的速度为v2,由机械能守恒定律有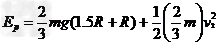
解得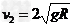
同理有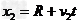
联立方程解得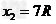
鱼饵能够落到水面的最大面积S