问题
计算题
如图所示，x轴与水平传送带重合，坐标原点O在传送带的左端，传送带长L＝8 m，匀速运动的速度v0＝5 m/s。一质量m＝1 kg的小物块轻轻放在传送带上xP＝2 m的P点，小物块随传送带运动到Q点后冲上光滑斜面且刚好到达N点。(小物块到达N点后被收集，不再滑下)若小物块经过Q处无机械能损失，小物块与传送带间的动摩擦因数μ＝0.5，重力加速度g＝10 m/s2。求：
(1)N点的纵坐标；
(2)小物块在传送带上运动产生的热量；
(3)若将小物块轻轻放在传送带上的某些位置，最终均能沿光滑斜面越过纵坐标yM＝0.5 m的M点，求这些位置的横坐标范围。
答案
解：(1)小物块在传送带上匀加速运动的加速度a＝μg＝5 m/s2 ①
小物块与传送带共速时，所用的时间t＝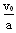
＝1 s ②
运动的位移Δx＝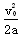
＝2.5 m＜(L－xP)＝6 m ③
故小物块与传送带达到相同速度后以v0＝5 m/s的速度匀速运动到Q，然后冲上光滑斜面到达N点，由机械能守恒定律得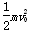
＝mgyN ④
解得yN＝1.25 m ⑤
(2)小物块在传送带上相对传送带滑动的位移s＝v0t－Δx＝2.5 m ⑥
产生的热量Q＝μmgs＝12.5 J ⑦
(3)设在坐标为x1处轻轻将小物块放在传送带上，最终刚能到达M点，由能量守恒得μmg(L－x1)＝mgyM ⑧
代入数据解得x1＝7 m ⑨
故小物块放在传送带上的位置坐标范围0≤x＜7 m ⑩