问题
计算题
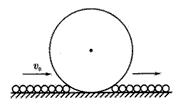
光滑水平面上有一条长为L的细铁链，初速度为v0，在铁链长度方向上向右滑动，遇到一个内侧带有光滑槽沟的竖直放置的圆环状轨道（在最下方错开）．圆环半径为R，且L> 2πR，铁链能滑上轨道完成圆周运动又向右滑去，如图所示，求最小初速v0．
答案
解：铁链的某一节恰好达最高点时，m0g=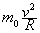
，在最高点的速度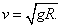
只能运用能量转化和守恒的观点我们才能得出：重力势能最大时，动能最小．而只有铁链占满整个圆环时，重力势能最大．
铁链全占满圆环时，在圆环上铁链的质量m=
（M为整条铁链的质量），
对整条铁链运用机械能守恒定律
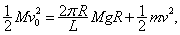
解得
，这就是最小的初速度。