问题
计算题
如图所示，将半径为R、圆心为O的大圆环固定在竖直的平面内，将两个轻质小圆环套在大圆环上，一根轻质长绳穿过两个小圆环，它的两端都系上质量为m1的重物，忽略小圆环的大小。求：
(1) 将两个小圆环固定在大圆环竖直对称轴的两侧倾角θ=30°的位置上。在两个小圆环间的绳子中点C处，挂上一个质量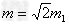
的重物，使两个小圆环间的绳子水平，然后无初速度释放重物m，设绳子与大、小圆环间的摩擦均可忽略，求重物m下降的最大距离。
(2)若不挂重物m，小圆环可以在大圆环上自由移动，且绳子与大、小圆环间及大小圆环之间的摩擦力均可以忽略，问两个小圆环分别在哪些位置时，系统可处于平衡状态？
答案
解：(1)重物向下先做加速运动，后做减速运动
当重物的速度为0时，下降的距离最大
设下降的最大距离为h
由机械能守恒定律得mgh=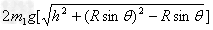
解得h=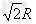
（另解h=0舍去）
(2)系统处于平衡状态时，两个小圆环的可能位置为：
两个小圆环同时位于大圆环的顶端
两个小圆环同时位于大圆环的底端
两个小圆环一个位于大圆环的顶端
另一个位于大圆环的底端
除上述三种情况外，根据对称性可知，系统如能平衡
则两个小圆环的位置一定关于大圆环竖直的对称轴对称
设平衡时，两个小圆环在大圆环竖直对称轴两侧α角的位置上（如下图所示）
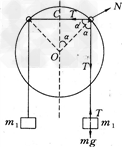
对于重物m，受绳子拉力T与重力mg的作用，有T=mg
对于小圆环，它受到三个力的作用
水平绳子的拉力T，竖直绳子的拉力T，大圆环的支持力N
两条绳子的拉力沿大圆环切向的分力大小相等，方向相反
有Tsinα= Tsinα'，得α'=α，而α+α'=90°，所以α=45°