问题
问答题
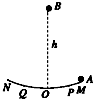
如图所示,在水平地面上有一段光滑圆弧形槽,弧的半径是R,所对圆心角小于10°,现在圆弧的右侧边缘M处放一个小球A,使其由静止下滑,则
(1)若在MN圆弧上存在两点P、Q,且P、Q关于O对称,且已测得球A由P直达Q所需时间为△t,则球由Q至N的最短时间为多少?
(2)若在圆弧的最低点O的正上方h处由静止释放小球B,让其自由下落,同时A球从圆弧右侧由静止释放,欲使A、B两球在圆弧最低点O处相遇,则B球下落的高度h是多少?
答案
(1)A做简谐运动
T=2πR g
则球由Q至N的最短时间
tmin=
-T 4
=△t 2 π 2
-R g △t 2
(2)B做自由落体下落的高度h
h=
gt21 2
若两球能够相遇则有
t=
T+n 2 T 4
得:h=
(n+1 2
)2R (n=1,2,3,4…) 1 2
答:
(1)球由Q至N的最短时间为π 2
-R g
.△t 2
(2)B球下落的高度h=
(n+1 2
)2R (n=1,2,3,4…)1 2
