问题
问答题
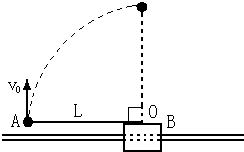
如图所示,质量为M的滑块B套在光滑的水平杆上可自由滑动,质量为m的小球A用一长为L的轻杆与B上的O点相连接,轻杆处于水平位置,可绕O点在竖直面内自由转动.
(1)固定滑块B,给小球A一竖直向上的初速度,使轻杆绕O点转过90°,则小球初速度的最小值是多少?
(2)若M=2m,不固定滑块B,给小球A一竖直向上的初速度v0,则当轻杆绕O点转过90°A球运动至最高点时,B球的速度多大?
答案
(1)小球A连着的是轻杆,所以能通过最高点的条件为:v1≥0
由机械能守恒定律得
mv02=mgL+1 2
mv121 2
所以 v0≥2gL
即小球初速度得最小值是2gL
(2)滑块B不固定时,A、B组成的系统水平方向所受的合力为零,所以水平方向动量守恒.设A运动到最高点时A、B的速度分别为vA、vB,
则由动量守恒和机械能守恒定律得
mvA-MvB=0
mv02=mgL1 2
mvA2+1 2
MvB21 2
M=2m
解方程组得 vB=
-2gLv 20 6
答:(1)固定滑块B,给小球A一竖直向上的初速度,使轻杆绕O点转过90°,则小球初速度的最小值是2gL
(2)若M=2m,不固定滑块B,给小球A一竖直向上的初速度v0,则当轻杆绕O点转过90°A球运动至最高点时,B球的速度是
.
-2gLv 20 6
