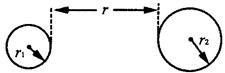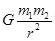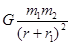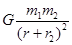问题
解答题
已知函数f(x)=sin(x-
(I)若α是第一象限角,且f(α)=
(II)求使f(x)≥g(x)成立的x的取值集合. |
答案
:∵sin(x-
)=sinxcosπ 6
-cosxsinπ 6
=π 6
sinx-3 2
cosx1 2
cos(x-
)=cosxcosπ 3
+sinxsinπ 3
=π 3
cosx+1 2
sinx3 2
∴f(x)=sin(x-
)+cos(x-π 6
)=(π 3
sinx-3 2
cosx)+(1 2
cosx+1 2
sinx)=3 2
sinx3
而g(x)=2sin2
=1-cosxx 2
(I)∵f(α)=
,∴3 3 5
sinα=3
,解之得sinα=3 3 5 3 5
∵α是第一象限角,∴cosα=
=1-sin2α 4 5
因此,g(α)=2sin2
=1-cosα=α 2
,1 5
(II)f(x)≥g(x),即
sinx≥1-cosx3
移项,得
sinx+cosx≥1,化简得2sin(x+3
)≥1π 6
∴sin(x+
)≥π 6
,可得1 2
+2kπ≤x+π 6
≤π 6
+2kπ(k∈Z)5π 6
解之得2kπ≤x≤
+2kπ(k∈Z)2π 3
因此,使f(x)≥g(x)成立的x的取值集合为{x|2kπ≤x≤
+2kπ(k∈Z)}2π 3

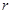 ,而球质量分布均匀,大小分别为
,而球质量分布均匀,大小分别为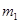 、
、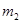 ,则两球间的万有引力的大小为( )
,则两球间的万有引力的大小为( )