问题
选择题
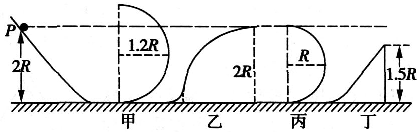
如图所示,小球从距地面高度为2R的斜面上P点无初速度释放,分别滑上甲、乙、丙、丁四个轨道,甲为半径为1.2R的半圆轨道,乙为半径为2R的
圆轨道、轨道和地面连接处有一段小圆弧,丙为半径为R的半圆轨道,丁为高为l.5R的斜面、斜面和地面连接处有一段小圆弧,所有接触面均光滑,则滑上四个轨道后运动到的最高点能和P等高的是( )1 4
A.甲
B.乙
C.丙
D.丁
答案
A、根据机械能守恒可知小球到达和P等高的位置时的速度为0,小球沿轨道甲内表面运动时,能通过最到点的条件为v≥
,因此小球不会到达和P等高的位置;故A错误.1.2gR
B、当小球恰好通过最高点时,轨道的支持力为零,则有mg=m
,则得v=v2 2R
,则小球能通过最高点的条件为v≤2gR
,根据机械能守恒得:小球到达最高点时的速度为零,故可以到达和P等高的位置;故B正确.2gR
C、小球能通过圆轨道丙内表面最高点的条件为v≥
,因此小球不会到达和P等高的位置.故C错误.gR
D、小球从斜面滑出后做斜上抛运动,水平方向做匀速运动,到最高点时速度不等于零,则根据机械能守恒得知,小球达到的最大高度小于2R.故D错误.
故选B
