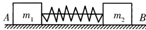
如图所示,滑块A、B的质量分别为m1与m2,m1<m2,由轻质弹簧相连接置于水平的气垫导轨上,用一轻绳把两滑块拉至最近,使弹簧处于最大压缩状态后绑紧.两滑块一起以恒定的速率v0向右滑动.突然轻绳断开.当弹簧伸至本身的自然长度时,滑块A的速度正好为0.求:
(1)绳断开到第一次恢复自然长度的过程中弹簧释放的弹性势能Ep;
(2)在以后的运动过程中,滑块B是否会有速度为0的时刻?试定量分析证明.
(1)当弹簧处压缩状态时,系统的机械能等于两滑块的动能和弹簧的弹性势能之和,当弹簧伸长到自然长度时,弹性势能为0,因这时滑块A的速度为0,故系统的机械能等于滑块B的动能.设这时滑块B的速度为v,则有E=
m2v2,1 2
因系统所受外力为0,由动量守恒定律(m1+m2)v0=m2 v,解得E=
;(m1+m2)2 v 20 2m2
由于只有弹簧的弹力做功,系统的机械能守恒
(m1+m2)v02+EP=E,解得EP=1 2
;m1(m1+m2) v 20 2m2
(2)假设在以后的运动中滑块B可以出现速度为0的时刻,并设此时A的速度为v1,
弹簧的弹性势能为Ep′,由机械能守恒定律得
m1v12+EP′=1 2
,(m1+m2) v 20 2m2
根据动量守恒得(m1+m2) v0=m1 v1,
求出v1代入上式得:
+EP′=(m1+m2) v 20 2m1
,(m1+m2) v 20 2m2
因为Ep′≥0,故得:
≤(m1+m2) v 20 2m1
;(m1+m2) v 20 2m2
即m1≥m2,这与已知条件中m1<m2不符.可见在以后的运动中不可能出现滑块B的速度为0的情况.
答:(1)绳断开到第一次恢复自然长度的过程中弹簧释放的弹性势能得EP=
;m1(m1+m2) v 20 2m2
(2)在以后的运动中不可能出现滑块B的速度为0的情况.
