问题
问答题
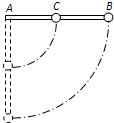
如图所示在一根细棒的中点C和端点B,分别固定两个质量、体积完全相同的小球,棒可以绕另一端A在竖直平面内无摩擦地转动.若从水平位置由静止释放,求两球到达最低位置时线速度的大小.小球的质量为m,棒的长度为L,质量不计..某同学对此题的解法是:
设最低位置时B球和C球的速度大小分别为v1、v2,运动过程中只有重力对小球做功,所以每个球的机械能都守恒.:
C球有
m1 2
=mgv 21
,v1=L 2 gL
B球有
m1 2
=mgL,v2=v 22 2gL
你同意上述解法吗?若不同意,请简述理由并求出你认为正确的答案.
答案
我不同意上述解法.
在转动过程中,B、C两球的角速度相同,设B球的速度为vB,C球的速度为vC,则有
vB=2vC ①
以B、C和杆组成的系统机械能守恒,由机械能守恒定律,并选最低点为零势能参考平面,则有
E1=mg?L+mg?L=2mgL,
E2=mg
+L 2
mvB2+1 2
mvC2②1 2
E1=E2 ③
由①②③式结合可以求出
vB=
gL12 5
vC=
gL3 5
答:两球到达最低位置时线速度的大小分别为:vB=
;vC=
gL12 5
gL3 5
