问题
问答题
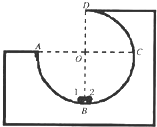
如图所示,在水平面上固定一个半径R=1m的3/4光滑圆弧轨道的工件,其圆心在O点,AOC连线水平,BOD连线竖直.在圆周轨道的最低点B有两个质量分别为m1=4kg,m 2=1kg的可视为质点的小球1和2,两小球间夹有一个极短的轻弹簧,当弹簧储存了EP=90J的弹性势能时锁定弹簧.某时刻解除锁定,弹簧将两个小球弹开,重力加速度g=10m/s2,试求:
(1)两小球脱离弹簧瞬间的速度
(2)通过计算说明小球2第一次沿轨道上滑过程中能否到达D点?
答案
(1)设小球m1的速度为v1,m2的速度为v2,两个小球与弹簧组成的系统,水平方向合外力为零,且只有弹力做功,由动量守恒定律,有:
m1v1=m2v2 ①
由机械能守恒定律,有;
Ep=
m1v12+1 2
m2v22 ②1 2
联立①②并代入数据解得:v1=3m/s向左
v2=12m/s向右
(2)小球2向右运动,设其能到达原周额最高点D,由机械能守恒,有:
m21 2
=m2g?2R+v 22
m21 2 v 2D
代入数据解得:vD=
m/s104
又小球能通过竖直面内光滑圆周最高点的条件为:
mg=mv2 R
代入数据解得:v=
m/s10
由于v<vD,故小球2能通过最高点.
答:(1)两小球脱离弹簧瞬间的速度分别为:3m/s向左、12m/s向右;
(2)小球2第一次沿轨道上滑过程中能到达D点.
