（1）长直杆的下端运动到碗的最低点时，长直杆在竖直方向的速度为0，而B、C沿水平方向运动，设速度为v_B=v_C=v．由机械能守恒定律得

   mgR=

1

2

?3mv²

解得，v_B=v_C=v=

2 3 gR

（2）A滑到最低点前，对B始终存在弹力，有向右的水平分量，故在此之前，BC共同加速不分离．

   设A沿竖直方向运动，速度为v_A，B、C沿水平方向运动，速度为v_B=v_C，且A杆的位置用θ表示，θ为碗面的球 心O至A杆下端与球面接触点的连线方向与竖直方向的夹角．

v_A，v_B的速度矢量图如图中平行四边形所示，由图得

   v_B=v_Acotθ

由机械能守恒得 mgR=

1

2

m

v

2A

+

1

2

2m

v

2B

+

1

2

m

v

2C

解得 v_A=

2gRcosθ 1+3cot2θ

，v_B=v_C=

2gRcosθcot2θ 1+3cot2θ

当滑到

R

2

处时，θ=60°，则得v_A=

gR 2

，v_B=v_C=

gR 6

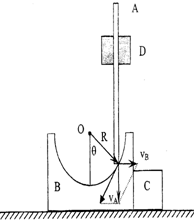
   当长直杆越过最低点后，B和C分离，长直杆的下端上升到所能达到的最高点时，长直杆在竖直方向上的速度为零．

  则有

1

2

2mv2=mgh，h=

2

3

R

则到

R

2

处A和B机械能守恒，则得

 

1

2

?2m

v

2B

=mg

R

2

+

1

2

m

v

′2A

+

1

2

2m

v

′2B

又v_B′=v_A′cotθ

解得 v_A′=

1 5 gR

，v_B′=

1 15 gR

，v_C′=

2 3 gR

答：

（1）当长直杆A的下端运动到碗的最低点时，长直杆A的速度

gR 2

，B、C的速度均为

gR 6

．

（2）当长直杆A的下端运动到距半球形碗的最低点

R

2

处，当长直杆越过最低点前时，长直杆A、B、C的速度分别为

1 5 gR

，

1 15 gR

，

2 3 gR

；当长直杆越过最低点后，分别为

1 5 gR

，

1 15 gR

，

2 3 gR

．