问题
解答题
已知函数f(x)=Asin(ωx+φ)+
(1)试求这条曲线的函数表达式; (2)求函数的对称中心; (3)用”五点法”画出(1)中函数在[0,π]上的图象; (4)试说明y=sin2x的图象是由y=f(x)的图象经过怎样的变换得到的? |
答案
(1)∵函数f(x)=Asin(ωx+φ)+
最高点的坐标为(2
,2π 8
),2
则此点到相邻最低点间的曲线与平衡轴交于点(
π,0),3 8
∴A=
,2
=T 4
,π 4
∴T=π,ω=2
∴f(x)=
sin(2x+φ)+2 2
∵过(
,2π 8
)点,2
∴2
=2
sin(2x+φ)+2 2
∵φ∈(-
,π 2
).π 2
∴φ=
,π 4
∴函数的解析式是f(x)=
sin(2x+2
)+π 4 2
(2)∵正弦曲线的对称中心是(kπ,0)
∴2x+
=kπ,k∈zπ 4
∴x=
-kπ 2
,π 8
∴函数的对称中心是(
-kπ 2
,π 8
)2
(3)
| x | 0 |
|
|
|
| π | ||||||||||
| 2x+ |
|
| π |
| 2π |
| ||||||||||
| f(x) | 1+
| 2
|
| 0 |
| 1+
|
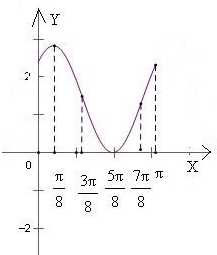
图形如右图
(4)y=f(x)先向下平移
个单位得到2
f(x)=
sin(2x+2
)再横标不变纵标变化为原来的π 4
得到2 2
f(x)=sin(2x+
)再向右平移π 4
个单位得到y=sin2xπ 8
