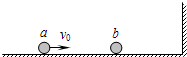
如图所示,光滑水平面上有两个质量分别为m1、m2的小球a、b,球a以水平速度vo=1m/s向右匀速运动,球b处于静止状态.两球右侧有一竖直墙壁,假设两球之间、球与墙壁之间发生正碰时均无机械能损失,为了使两球能发生、而且只能发生两次碰撞,试讨论两球的质量之比m1/m2应满足什么条件.
设球a和球b第一次碰撞后速度分别为v1和v2,取向右为正方向.
由系统动量守恒:m1v0=m1v1+m2v2…①
系统机械能守恒得:m1v02=m1v12+m2v22…②
解得:v1=v2=…③
讨论情况分别如下:
(1)、当m1>m2时,碰后a、b两球均向右运动,当球b与墙壁碰后以速度v2返回,并将与球a发生第二次碰撞,设碰后两球速度分别为v1′,v2′则有:
m1v1+m2(-v2)=m1v1′+m2v2′
m1v12+m2v22=m1v1′2+m2v2′2
解得:v1′=…④
v2′=…⑤
因为m1>m2,故第二次碰后球b向右运动将再次与墙相碰,并以v2′返回;若要球a和球b不发生第三次碰撞,则应满足 v1′<0 且v2′≤|v'1|
即 (m1-m2)2-4m1m2<0 且4m1(m1-m2)≤|(m1-m2)2-4m1m2|…⑥
解得:3-2<<3+2且1-≤≤1+…⑦
再加上条件m1>m2 得:1<≤1+…⑧
(2)、m1=m2时,由①②得v1=0,v2=1m/s球b与墙壁碰后以速度1m/s返回与球a第二次碰撞,碰后a球以1m/s的速度向左运动,b球静止,此后两球不再相碰…⑨
(3)、m1<m2时,由①②可知v1<0,v2>0,即a球向左运动,球b向右运动并与墙壁碰后原速弹回,要使球b与球a发生第二次碰撞,应满足:
v2>-v1 即:2m1>-(m1-m2),得>…⑩
因m1<m2,故两球第二次相碰后,球a向左运动的速度必大于球b向左的运动速度,此后两球不再发生碰撞.
综合(1)(2)(3)得满足范围:<≤1+…
答:两球的质量满足范围:<≤1+.