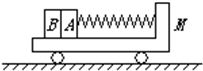
质量为M=6kg的小车放在光滑的水平面上,物块A和B的质量均为m=2kg,且均放在小车的光滑水平底板上,物块A和小车右侧壁用一根轻弹簧连接,不会分离,如图所示,物块A和B并排靠在一起,现用力向右压B,并保持小车静止,使弹簧处于压缩状态,在此过程中外力做功270J.撤去外力,当A和B分开后,在A达到小车底板的最左端位置之前,B已从小车左端抛出,求:
(1)B与A分离时,小车的速度是多大?
(2)从撤去外力至B与A分离时,A对B做了多少功?
(3)假设弹簧伸长到最长时B已离开小车,A仍在车上,那么此时弹簧的弹性势能是多大?
(1)当弹簧第一次恢复原长时,B与A恰好分离,此时B与A有相同速度设为v1,小车速度为v2,根据动量守恒定律,有 2mv1=Mv2
又由能量关系,有 2×
m1 2
+v 21
M1 2
=270v 22
解得:v1=9m/s v2=6m/s 即小车速度为6m/s.
(2)根据动能定理,从撤去外力至B与A分离时,A对B做的功为W=
m1 2
=81Jv 21
(3)B与A分离后速度不变,弹簧伸到最长时,A与小车速度相同,设为v3,则有:
mv1=(m+M)v3
m1 2
+v 21
(m+M)1 2
+Ep=270v 23
联立解得:v3=2.25m/s,Ep=168.75J.
答:(1)B与A分离时,小车的速度是6m/s;
(2)从撤去外力至B与A分离时,A对B做了81J的功;
(3)假设弹簧伸长到最长时B已离开小车,A仍在车上,那么此时弹簧的弹性势能是168.75J.
